https://en.wikipedia.org/wiki/Quantum_field_theory
| Quantum field theory |
|---|
|
| History |
Contents
- 1 Motivation and history
- 2 Representation of physical reality
- 3 Particle-path interpretation
- 4 Description
- 5 Canonical quantization formulation
- 6 Path integral formulation
- 7 Particle-path representation
- 8 Nonperturbative effects
- 9 In popular culture
- 10 See also
- 11 Notes
- 12 References
- 13 External links
Feynman diagram
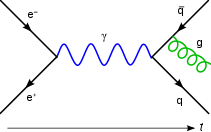
In theoretical physics, Feynman diagrams are pictorial representations of the mathematical expressions describing the behavior of subatomic particles.In this Feynman diagram, an electron and a positron annihilate, producing a photon (represented by the blue sine wave) that becomes a quark–antiquark pair, after which the antiquark radiates a gluon (represented by the green helix).
The scheme is named after its inventor, American physicist Richard Feynman, and was first introduced in 1948.
The interaction of sub-atomic particles can be complex and difficult to understand intuitively. Feynman diagrams give a simple visualization of what would otherwise be a rather arcane and abstract formula.
As David Kaiser writes, "since the middle of the 20th century, theoretical physicists have increasingly turned to this tool to help them undertake critical calculations", and so "Feynman diagrams have revolutionized nearly every aspect of theoretical physics".[1]
While the diagrams are applied primarily to quantum field theory, they can also be used in other fields, such as solid-state theory.
Feynman used Ernst Stueckelberg's interpretation of the positron as if it were an electron moving backward in time.[2] Thus, antiparticles are represented as moving backward along the time axis in Feynman diagrams.
The calculation of probability amplitudes in theoretical particle physics requires the use of rather large and complicated integrals over a large number of variables.
These integrals do, however, have a regular structure, and may be represented graphically as Feynman diagrams.
A Feynman diagram is a contribution of a particular class of particle paths, which join and split as described by the diagram.
More precisely, and technically, a Feynman diagram is a graphical representation of a perturbative contribution to the transition amplitude or correlation function of a quantum mechanical or statistical field theory.
Within the canonical formulation of quantum field theory, a Feynman diagram represents a term in the Wick's expansion of the perturbative S-matrix.
Alternatively, the path integral formulation of quantum field theory represents the transition amplitude as a weighted sum of all possible histories of the system from the initial to the final state, in terms of either particles or fields.
The transition amplitude is then given as the matrix element of the S-matrix between the initial and the final states of the quantum system.
Feynman used Ernst Stueckelberg's interpretation of the positron as if it were an electron moving backward in time.[2]
Thus, antiparticles are represented as moving backward along the time axis in Feynman diagrams.
Motivation and history
In this diagram, a kaon, made of an up and anti-strange quark, decays both weakly and strongly into three pions, with intermediate steps involving a W boson and a gluon (represented by the blue sine wave and green spiral, respectively).
1 aubust 2017
In theoretical physics, Feynman diagrams are pictorial representations of the mathematical expressions describing the behavior of subatomic particles.
The scheme is named after its inventor, American physicist Richard Feynman, and was first introduced in 1948. The interaction of sub-atomic particles can be complex and difficult to understand intuitively. Feynman diagrams give a simple visualization of what would otherwise be a rather arcane and abstract formula. As David Kaiser writes, "since the middle of the 20th century, theoretical physicists have increasingly turned to this tool to help them undertake critical calculations", and so "Feynman diagrams have revolutionized nearly every aspect of theoretical physics".[1]
While the diagrams are applied primarily to quantum field theory, they can also be used in other fields, such as solid-state theory.
Feynman used Ernst Stueckelberg's interpretation of the positron as if it were an electron moving backward in time.[2]
Thus, antiparticles are represented as moving backward along the time axis in Feynman diagrams.
The calculation of probability amplitudes in theoretical particle physics requires the use of rather large and complicated integrals over a large number of variables. These integrals do, however, have a regular structure, and may be represented graphically as Feynman diagrams.
A Feynman diagram is a contribution of a particular class of particle paths, which join and split as described by the diagram. More precisely, and technically, a Feynman diagram is a graphical representation of a perturbative contribution to the transition amplitude or correlation function of a quantum mechanical or statistical field theory. Within the canonical formulation of quantum field theory, a Feynman diagram represents a term in the Wick's expansion of the perturbative S-matrix. Alternatively, the path integral formulation of quantum field theory represents the transition amplitude as a weighted sum of all possible histories of the system from the initial to the final state, in terms of either particles or fields. The transition amplitude is then given as the matrix element of the S-matrix between the initial and the final states of the quantum system.
Quantum field theory 
History Contents
- 1 Motivation and history
- 2 Representation of physical reality
- 3 Particle-path interpretation
- 4 Description
- 5 Canonical quantization formulation
- 6 Path integral formulation
- 7 Particle-path representation
- 8 Nonperturbative effects
- 9 In popular culture
- 10 See also
- 11 Notes
- 12 References
- 13 External links


No comments:
Post a Comment