1 august 2017.
Maxwell's equations
Maxwell's equations (mid-left) as featured on a monument in front of Warsaw University's Center of New Technologies
The equations have two major variants. The microscopic Maxwell equations have universal applicability, but are unwieldy for common calculations. They relate the electric and magnetic fields to total charge and total current, including the complicated charges and currents in materials at the atomic scale. The "macroscopic" Maxwell equations define two new auxiliary fields that describe the large-scale behaviour of matter without having to consider atomic scale details. However, their use requires experimentally determining parameters for a phenomenological description of the electromagnetic response of materials.
The term "Maxwell's equations" is often used for equivalent alternative formulations. Versions of Maxwell's equations based on the electric and magnetic potentials are preferred for explicitly solving the equations as a boundary value problem, analytical mechanics, or for use in quantum mechanics. The spacetime formulations (i.e., on spacetime rather than space and time separately), are commonly used in high energy and gravitational physics because they make the compatibility of the equations with special and general relativity manifest.[note 1] In fact, Einstein developed special and general relativity to accommodate the absolute speed of light that drops out of the Maxwell equations with the principle that only relative movement has physical consequences.
Since the mid-20th century, it has been understood that Maxwell's equations are not exact, but a classical field theory approximation of some aspects of the fundamental theory of quantum electrodynamics, although some quantum features, such as quantum entanglement, are completely absent and in no way approximated. (For example, quantum cryptography has no approximate version in Maxwell theory.) In many situations, though, deviations from Maxwell's equations are immeasurably small. Exceptions include nonclassical light, photon–photon scattering, quantum optics, and many other phenomena related to photons or virtual photons.
Contents
- 1 Formulation in terms of electric and magnetic fields (microscopic or in vacuum version)
- 2 Relationship between differential and integral formulations
- 3 Conceptual descriptions
- 4 Charge conservation
- 5 Vacuum equations, electromagnetic waves and speed of light
- 6 Macroscopic formulation
- 7 Alternative formulations
- 8 Relativistic formulations
- 9 Solutions
- 10 Overdetermination of Maxwell's equations
- 11 Limitations of the Maxwell equations as a theory of electromagnetism
- 12 Variations
- 13 See also
- 14 Notes
- 15 References
- 16 Historical publications
- 17 External links
Formulation in terms of electric and magnetic fields (microscopic or in vacuum version)
In the electric and magnetic field formulation there are four equations. The two inhomogeneous equations describe how the fields vary in space due to sources. Gauss's law describes how electric fields emanate from electric charges. Gauss's law for magnetism describes magnetic fields as closed field lines not due to magnetic monopoles. The two homogeneous equations describe how the fields "circulate" around their respective sources. Ampère's law with Maxwell's addition describes how the magnetic field "circulates" around electric currents and time varying electric fields, while Faraday's law describes how the electric field "circulates" around time varying magnetic fields.A separate law of nature, the Lorentz force law, describes how the electric and magnetic field act on charged particles and currents. A version of this law was included in the original equations by Maxwell but, by convention, is no longer.
The precise formulation of Maxwell's equations depends on the precise definition of the quantities involved. Conventions differ with the unit systems, because various definitions and dimensions are changed by absorbing dimensionful factors like the speed of light c. This makes constants come out differently. The most common form is based on conventions used when quantities measured using SI units, but other commonly used conventions are used with other units including Gaussian units based on the cgs system,[1] Lorentz–Heaviside units (used mainly in particle physics), and Planck units (used in theoretical physics).
The vector calculus formulation below has become standard. It is mathematically much more convenient than Maxwell's original 20 equations and is due to Oliver Heaviside.[2][3] The differential and integral equations formulations are mathematically equivalent and are both useful. The integral formulation relates fields within a region of space to fields on the boundary and can often be used to simplify and directly calculate fields from symmetric distributions of charges and currents. On the other hand, the differential equations are purely local and are a more natural starting point for calculating the fields in more complicated (less symmetric) situations, for example using finite element analysis.[4] For formulations using tensor calculus or differential forms, see alternative formulations. For relativistically invariant formulations, see relativistic formulations.
Formulation in SI units convention
Name Integral equations Differential equations Meaning Gauss's law 
The electric flux leaving a volume is proportional to the charge inside. Gauss's law for magnetism 
There are no magnetic monopoles; the total magnetic flux through a closed surface is zero. Maxwell–Faraday equation (Faraday's law of induction) The voltage induced in a closed loop is proportional to the rate of change of the magnetic flux that the loop encloses. Ampère's circuital law (with Maxwell's addition) The magnetic field induced around a closed loop is proportional to the electric current plus displacement current (rate of change of electric field) that the loop encloses.
Formulation in Gaussian units convention
Gaussian units are a popular system of units, that are part of the centimetre–gram–second system of units (cgs). When using cgs units it is conventional to use a slightly different definition of electric field Ecgs = c−1 ESI. This implies that the modified electric and magnetic field have the same units (in the SI convention this is not the case making dimensional analysis of the equations different: e.g. for an electromagnetic wave in vacuum , ). The CGS system uses a unit of charge defined in such a way that the permittivity of the vacuum ε0 = 1/4πc, hence μ0 = 4π/c. These units are sometimes preferred over SI units in the context of special relativity,[5]:vii in which the components of the electromagnetic tensor,
the Lorentz covariant object describing the electromagnetic field, have
the same unit without constant factors. Using these different
conventions, the Maxwell equations become:[6]
, ). The CGS system uses a unit of charge defined in such a way that the permittivity of the vacuum ε0 = 1/4πc, hence μ0 = 4π/c. These units are sometimes preferred over SI units in the context of special relativity,[5]:vii in which the components of the electromagnetic tensor,
the Lorentz covariant object describing the electromagnetic field, have
the same unit without constant factors. Using these different
conventions, the Maxwell equations become:[6]Name Integral equations Differential equations Meaning Gauss's law 
The electric flux leaving a volume is proportional to the charge inside. Gauss's law for magnetism 
There are no magnetic monopoles; the total magnetic flux through a closed surface is zero. Maxwell–Faraday equation (Faraday's law of induction) The voltage induced in a closed loop is proportional to the rate of change of the magnetic flux that the loop encloses. Ampère's circuital law (with Maxwell's addition) The magnetic field integrated around a closed loop is proportional to the electric current plus displacement current (rate of change of electric field) that the loop encloses.
Key to the notation
Symbols in bold represent vector quantities, and symbols in italics represent scalar quantities, unless otherwise indicated.The equations introduce the electric field, E, a vector field, and the magnetic field, B, a pseudovector field, each generally having a time and location dependence. The sources are
- the total electric charge density (total charge per unit volume), ρ, and
- the total electric current density (total current per unit area), J.
- the permittivity of free space, ε0, and
- the permeability of free space, μ0.
Differential equations
In the differential equations,- the nabla symbol, ∇, denotes the three-dimensional gradient operator,
- the ∇⋅ symbol denotes the divergence operator,
- the ∇× symbol denotes the curl operator.
Integral equations
In the integral equations,- Ω is any fixed volume with closed boundary surface ∂Ω, and
- Σ is any fixed surface with closed boundary curve ∂Σ,

is a surface integral over the boundary surface ∂Ω, with the loop indicating the surface is closed
is a volume integral over the volume Ω,
is a line integral around the boundary curve ∂Σ, with the loop indicating the curve is closed.
is a surface integral over the surface Σ,
- The total electric charge Q enclosed in Ω is the volume integral over Ω of the charge density ρ (see the "macroscopic formulation" section below):
-
-
- where dV is the volume element.
- The net electric current I is the surface integral of the electric current density J passing through a fixed surface, Σ:
-
-
- where dS denotes the vector element of surface area S, normal to surface Σ. (Vector area is sometimes denoted by A rather than S, but this conflicts with the notation for magnetic potential).
Relationship between differential and integral formulations
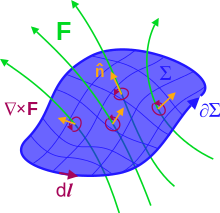
The equivalence of the differential and integral formulations are a consequence of the Gauss divergence theorem and the Kelvin–Stokes theorem.Flux and divergence
Volume Ω and its closed boundary ∂Ω, containing (respectively enclosing) a source (+) and sink (−) of a vector field F. Here, F could be the E field with source electric charges, but not the B field which has no magnetic charges as shown. The outward unit normal is n.
-

.
Circulation and curl
Surface Σ with closed boundary ∂Σ. F could be the E or B fields. Again, n is the unit normal. (The curl of a vector field doesn't literally look like the "circulations", this is a heuristic depiction.)
-
,
-
.
The line integrals and curls are analogous to quantities in classical fluid dynamics: the circulation of a fluid is the line integral of the fluid's flow velocity field around a closed loop, and the vorticity of the fluid is the curl of the velocity field.
Conceptual descriptions
Gauss's law
Gauss's law describes the relationship between a static electric field and the electric charges that cause it: The static electric field points away from positive charges and towards negative charges. In the field line description, electric field lines begin only at positive electric charges and end only at negative electric charges. 'Counting' the number of field lines passing through a closed surface, therefore, yields the total charge (including bound charge due to polarization of material) enclosed by that surface divided by dielectricity of free space (the vacuum permittivity). More technically, it relates the electric flux through any hypothetical closed "Gaussian surface" to the enclosed electric charge.
Gauss's law for magnetism:
magnetic field lines never begin nor end but form loops or extend to
infinity as shown here with the magnetic field due to a ring of current.
Gauss's law for magnetism
Gauss's law for magnetism states that there are no "magnetic charges" (also called magnetic monopoles), analogous to electric charges.[7] Instead, the magnetic field due to materials is generated by a configuration called a dipole. Magnetic dipoles are best represented as loops of current but resemble positive and negative 'magnetic charges', inseparably bound together, having no net 'magnetic charge'. In terms of field lines, this equation states that magnetic field lines neither begin nor end but make loops or extend to infinity and back. In other words, any magnetic field line that enters a given volume must somewhere exit that volume. Equivalent technical statements are that the sum total magnetic flux through any Gaussian surface is zero, or that the magnetic field is a solenoidal vector field.Faraday's law
In a geomagnetic storm,
a surge in the flux of charged particles temporarily alters Earth's
magnetic field, which induces electric fields in Earth's atmosphere,
thus causing surges in electrical power grids. (Not to scale.)
Ampère's law with Maxwell's addition
Maxwell's addition to Ampère's law is particularly important: it makes the set of equations mathematically consistent for non static fields, without changing the laws of Ampere and Gauss for static fields.[8] However, as a consequence, it predicts that a changing magnetic field induces an electric field and vice versa.[7][9] Therefore, these equations allow self-sustaining "electromagnetic waves" to travel through empty space (see electromagnetic wave equation).
The speed calculated for electromagnetic waves, which could be predicted from experiments on charges and currents,[note 2] exactly matches the speed of light; indeed, light is one form of electromagnetic radiation (as are X-rays, radio waves, and others). Maxwell understood the connection between electromagnetic waves and light in 1861, thereby unifying the theories of electromagnetism and optics.
Charge conservation
The invariance of charge can be derived as a corollary of Maxwell's equations. The left hand side of the modified Ampere's Law has zero divergence by the div–curl identity. Combining the right hand side, Gauss's law, and interchange of derivatives gives:-
.
Vacuum equations, electromagnetic waves and speed of light
This 3D diagram shows a plane linearly polarized wave propagating from left to right with the same wave equations where E = E0 sin(−ωt + k ⋅ r) and B = B0 sin(−ωt + k ⋅ r)
In addition, E and B are mutually perpendicular to each other and the direction of wave propagation, and are in phase with each other. A sinusoidal plane wave is one special solution of these equations. Maxwell's equations explain how these waves can physically propagate through space. The changing magnetic field creates a changing electric field through Faraday's law. In turn, that electric field creates a changing magnetic field through Maxwell's addition to Ampère's law. This perpetual cycle allows these waves, now known as electromagnetic radiation, to move through space at velocity c.
Macroscopic formulation
The above equations are the "microscopic" version of Maxwell's equations, expressing the electric and the magnetic fields in terms of the (possibly atomic-level) charges and currents present. This is sometimes called the "general" form, but the macroscopic version below is equally general, the difference being one of bookkeeping.The microscopic version is sometimes called "Maxwell's equations in a vacuum": this refers to the fact that the material medium is not built into the structure of the equations, but appears only in the charge and current terms. The microscopic version was introduced by Lorentz, who tried to use it to derive the macroscopic properties of bulk matter from its microscopic constituents.[10]:5
"Maxwell's macroscopic equations", also known as Maxwell's equations in matter, are more similar to those that Maxwell introduced himself.
Name Integral equations (SI convention) Differential equations (SI convention) Differential equations (Gaussian convention) Gauss's law 
Gauss's law for magnetism 
Maxwell–Faraday equation (Faraday's law of induction) Ampère's circuital law (with Maxwell's addition)
The cost of this factorization is that additional fields, the displacement field D and the magnetizing field H, are defined and need to be determined. Phenomenological constituent equations relate the additional fields to the electric field E and the magnetic B-field, often through a simple linear relation.
For a detailed description of the differences between the microscopic (total charge and current including material contributes or in air/vacuum)[note 4] and macroscopic (free charge and current; practical to use on materials) variants of Maxwell's equations, see below.
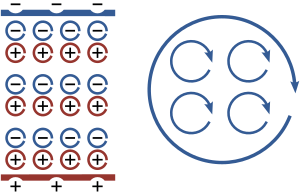
Bound charge and current
Left: A schematic view of how an assembly of microscopic dipoles produces opposite surface charges as shown at top and bottom. Right:
How an assembly of microscopic current loops add together to produce a
macroscopically circulating current loop. Inside the boundaries, the
individual contributions tend to cancel, but at the boundaries no
cancelation occurs.
Somewhat similarly, in all materials the constituent atoms exhibit magnetic moments that are intrinsically linked to the angular momentum of the components of the atoms, most notably their electrons. The connection to angular momentum suggests the picture of an assembly of microscopic current loops. Outside the material, an assembly of such microscopic current loops is not different from a macroscopic current circulating around the material's surface, despite the fact that no individual charge is traveling a large distance. These bound currents can be described using the magnetization M.[12]
The very complicated and granular bound charges and bound currents, therefore, can be represented on the macroscopic scale in terms of P and M which average these charges and currents on a sufficiently large scale so as not to see the granularity of individual atoms, but also sufficiently small that they vary with location in the material. As such, Maxwell's macroscopic equations ignore many details on a fine scale that can be unimportant to understanding matters on a gross scale by calculating fields that are averaged over some suitable volume.
Auxiliary fields, polarization and magnetization
The definitions (not constitutive relations) of the auxiliary fields are:Constitutive relations
In order to apply 'Maxwell's macroscopic equations', it is necessary to specify the relations between displacement field D and the electric field E, as well as the magnetizing field H and the magnetic field B. Equivalently, we have to specify the dependence of the polarisation P (hence the bound charge) and the magnetisation M (hence the bound current) on the applied electric and magnetic field. The equations specifying this response are called constitutive relations. For real-world materials, the constitutive relations are rarely simple, except approximately, and usually determined by experiment. See the main article on constitutive relations for a fuller description.[13]:44–45For materials without polarisation and magnetisation, the constitutive relations are (by definition)[5]:2
An alternative viewpoint on the microscopic equations is that they are the macroscopic equations together with the statement that vacuum behaves like a perfect linear "material" without additional polarisation and magnetisation. More generally, for linear materials the constitutive relations are[13]:44–45
 , however, the linear approximation can break down in common materials like iron leading to phenomena like hysteresis. Even the linear case can have various complications, however.
, however, the linear approximation can break down in common materials like iron leading to phenomena like hysteresis. Even the linear case can have various complications, however.- For homogeneous materials, ε and μ are constant throughout the material, while for inhomogeneous materials they depend on location within the material (and perhaps time).[14]:463
- For isotropic materials, ε and μ are scalars, while for anisotropic materials (e.g. due to crystal structure) they are tensors.[13]:421[14]:463
- Materials are generally dispersive, so ε and μ depend on the frequency of any incident EM waves.[13]:625[14]:397
In applications one also has to describe how the free currents and charge density behave in terms of E and B possibly coupled to other physical quantities like pressure, and the mass, number density, and velocity of charge-carrying particles. E.g., the original equations given by Maxwell (see History of Maxwell's equations) included Ohms law in the form
Alternative formulations
Following is a summary of some of the numerous other ways to write the microscopic Maxwell's equations, showing they can be formulated using different mathematical formalisms. In addition, we formulate the equations using "potentials". Originally they were introduced as a convenient way to solve the homogeneous equations, but it was originally thought that all the observable physics was contained in the electric and magnetic fields (or relativistically, the Faraday tensor). The potentials play a central role in quantum mechanics, however, and act quantum mechanically with observable consequences even when the electric and magnetic fields vanish (Aharonov–Bohm effect). See the main articles for the details of each formulation. SI units are used throughout.Formalism Formulation Homogeneous equations Inhomogeneous equations Vector calculus Fields 3D Euclidean space + time Potentials (any gauge) 3D Euclidean space + time Potentials (Lorenz gauge) 3D Euclidean space + time Tensor calculus Fields space + time
spatial metric independent of timePotentials space (with topological restrictions) + time
spatial metric independent of timePotentials (Lorenz gauge) space (with topological restrictions) + time
spatial metric independent of timeDifferential forms Fields Any space + time Potentials (any gauge) Any space (with topological restrictions) + time Potential (Lorenz Gauge) Any space (with topological restrictions) + time
spatial metric independent of time
- In the vector formulation on Euclidean space + time, φ is the electrical potential, and A is the vector potential.
Relativistic formulations
The Maxwell equations can also be formulated on a spacetime-like Minkowski space where space and time are treated on equal footing. The direct spacetime formulations make manifest that the Maxwell equations are relativistically invariant. Because of this symmetry electric and magnetic field are treated on equal footing and are recognised as components of the Faraday tensor. This reduces the four Maxwell equations to two, which simplifies the equations, although we can no longer use the familiar vector formulation. In fact the Maxwell equations in the space + time formulation are not Galileo invariant and have Lorenz invariance a hidden symmetry. This was a major source of inspiration for the development of relativity theory. The space + time formulation is not a non-relativistic approximation, however, they describe the same physics by simply renaming variables. For this reason the relativistic invariant equations are usually simply called the Maxwell equations as well.Formalism Formulation Homogeneous equations Inhomogeneous equations Tensor calculus Fields Minkowski space Potentials (any gauge) Minkowski space Potentials (Lorenz gauge) Minkowski space Fields Any spacetime Potentials (any gauge) Any spacetime (with topological restrictions) Potentials (Lorenz gauge) Any spacetime (with topological restrictions) Differential forms Fields Any spacetime Potentials (any gauge) Any spacetime (with topological restrictions) Potentials (Lorenz gauge) Any spacetime (with topological restrictions)
- In the tensor calculus formulation, the electromagnetic tensor Fαβ is an antisymmetric covariant rank 2 tensor; the four-potential, Aα, is a covariant vector; the current, Jα, is a vector; the square brackets, [ ], denote antisymmetrization of indices; ∂α is the derivative with respect to the coordinate, xα. In Minkowski space coordinates are chosen with respect to an inertial frame; (xα) = (ct,x,y,z), so that the metric tensor used to raise and lower indices is ηαβ = diag(1,−1,−1,−1). The d'Alembert operator on Minkowski space is ◻ = ∂α∂α as in the vector formulation. In general spacetimes, the coordinate system xα is arbitrary, the covariant derivative ∇α, the Ricci tensor, Rαβ and raising and lowering of indices are defined by the Lorentzian metric, gαβ and the d'Alembert operator is defined as ◻ = ∇α∇α. The topological restriction is that the second real cohomology group of the space vanishes (see the differential form formulation for an explanation). Note that this is violated for Minkowski space with a line removed, which can model a (flat) spacetime with a point-like monopole on the complement of the line.
- In the differential form formulation on arbitrary space times, F = Fαβdxα ∧ dxβ is the electromagnetic tensor considered as a 2-form, A = Aαdxα is the potential 1-form, J is the current 3-form, d is the exterior derivative, and
is the Hodge star on forms defined (up to its an orientation, i.e. its sign) by the Lorentzian metric of spacetime. The Hodge star
depends on the metric tensor only for its local scale. This means that, as formulated, the differential form field equations are conformally invariant, but the Lorenz gauge condition breaks conformal invariance. The operator
is the d'Alembert–Laplace–Beltrami operator on 1-forms on an arbitrary Lorentzian spacetime. The topological condition is again that the second real cohomology group is trivial. By the isomorphism with the second de Rham cohomology this condition means that every closed 2-form is exact.
Solutions
Maxwell's equations are partial differential equations that relate the electric and magnetic fields to each other and to the electric charges and currents. Often, the charges and currents are themselves dependent on the electric and magnetic fields via the Lorentz force equation and the constitutive relations. These all form a set of coupled partial differential equations, which are often very difficult to solve. In fact, the solutions of these equations encompass all the diverse phenomena in the entire field of classical electromagnetism. A thorough discussion is far beyond the scope of the article, but some general notes follow.Like any differential equation, boundary conditions[17][18][19] and initial conditions[20] are necessary for a unique solution. For example, even with no charges and no currents anywhere in spacetime, many solutions to Maxwell's equations are possible, not just the obvious solution E = B = 0. Another solution is E = constant, B = constant, while yet other solutions have electromagnetic waves filling spacetime. In some cases, Maxwell's equations are solved through infinite space, and boundary conditions are given as asymptotic limits at infinity.[21] In other cases, Maxwell's equations are solved in just a finite region of space, with appropriate boundary conditions on that region: For example, the boundary could be an artificial absorbing boundary representing the rest of the universe,[22][23] or periodic boundary conditions, or (as with a waveguide or cavity resonator) the boundary conditions may describe the walls that isolate a small region from the outside world.[24]
Jefimenko's equations (or the closely related Liénard–Wiechert potentials) are the explicit solution to Maxwell's equations for the electric and magnetic fields created by any given distribution of charges and currents. It assumes specific initial conditions to obtain the so-called "retarded solution", where the only fields present are the ones created by the charges. Jefimenko's equations are not so helpful in situations when the charges and currents are themselves affected by the fields they create.
Numerical methods for differential equations can be used to approximately solve Maxwell's equations when an exact solution is impossible. These methods usually require a computer, and include the finite element method and finite-difference time-domain method.[17][19][25][26][27] For more details, see Computational electromagnetics.
Overdetermination of Maxwell's equations
Maxwell's equations seem overdetermined, in that they involve six unknowns (the three components of E and B) but eight equations (one for each of the two Gauss's laws, three vector components each for Faraday's and Ampere's laws). (The currents and charges are not unknowns, being freely specifiable subject to charge conservation.) This is related to a certain limited kind of redundancy in Maxwell's equations: It can be proven that any system satisfying Faraday's law and Ampere's law automatically also satisfies the two Gauss's laws, as long as the system's initial condition does.[28][29] This explanation was first introduced by Julius Adams Stratton in 1941.[30] Although it is possible to simply ignore the two Gauss's laws in a numerical algorithm (apart from the initial conditions), the imperfect precision of the calculations can lead to ever-increasing violations of those laws. By introducing dummy variables characterizing these violations, the four equations become not overdetermined after all. The resulting formulation can lead to more accurate algorithms that take all four laws into account.[31]Limitations of the Maxwell equations as a theory of electromagnetism
While Maxwell's equations (along with the rest of classical electromagnetism) are extraordinarily successful at explaining and predicting a variety of phenomena, they are not exact, but approximations. In some special situations, they can be noticeably inaccurate. Examples include extremely strong fields (see Euler–Heisenberg Lagrangian) and extremely short distances (see vacuum polarization). Moreover, various phenomena occur in the world even though Maxwell's equations predict them to be impossible, such as "nonclassical light" and quantum entanglement of electromagnetic fields (see quantum optics). Finally, any phenomenon involving individual photons, such as the photoelectric effect, Planck's law, the Duane–Hunt law, single-photon light detectors, etc., would be difficult or impossible to explain if Maxwell's equations were exactly true, as Maxwell's equations do not involve photons. For the most accurate predictions in all situations, Maxwell's equations have been superseded by quantum electrodynamics.Variations
Popular variations on the Maxwell equations as a classical theory of electromagnetic fields are relatively scarce because the standard equations have stood the test of time remarkably well.Magnetic monopoles
Maxwell's equations posit that there is electric charge, but no magnetic charge (also called magnetic monopoles), in the universe. Indeed, magnetic charge has never been observed (despite extensive searches)[note 5] and may not exist. If they did exist, both Gauss's law for magnetism and Faraday's law would need to be modified, and the resulting four equations would be fully symmetric under the interchange of electric and magnetic fields.[5]:273–275See also
Notes
- See magnetic monopole for a discussion of monopole searches. Recently, scientists have discovered that some types of condensed matter, including spin ice and topological insulators, which display emergent behavior resembling magnetic monopoles. (See [1] and [2].) Although these were described in the popular press as the long-awaited discovery of magnetic monopoles, they are only superficially related. A "true" magnetic monopole is something where ∇ ⋅ B ≠ 0, whereas in these condensed-matter systems, ∇ ⋅ B = 0 while only ∇ ⋅ H ≠ 0.
References
- B Jiang & J Wu & L.A. Povinelli (1996). "The Origin of Spurious Solutions in Computational Electromagnetics". Journal of Computational Physics. 125 (1): 104. Bibcode:1996JCoPh.125..104J. doi:10.1006/jcph.1996.0082.
- Further reading can be found in list of textbooks in electromagnetism
Historical publications
- On Faraday's Lines of Force – 1855/56 Maxwell's first paper (Part 1 & 2) – Compiled by Blaze Labs Research (PDF)
- On Physical Lines of Force – 1861 Maxwell's 1861 paper describing magnetic lines of Force – Predecessor to 1873 Treatise
- James Clerk Maxwell, "A Dynamical Theory of the Electromagnetic Field", Philosophical Transactions of the Royal Society of London 155, 459–512 (1865). (This article accompanied a December 8, 1864 presentation by Maxwell to the Royal Society.)
- A Dynamical Theory Of The Electromagnetic Field – 1865 Maxwell's 1865 paper describing his 20 Equations, link from Google Books.
- J. Clerk Maxwell (1873) A Treatise on Electricity and Magnetism
- Maxwell, J.C., A Treatise on Electricity And Magnetism – Volume 1 – 1873 – Posner Memorial Collection – Carnegie Mellon University
- Maxwell, J.C., A Treatise on Electricity And Magnetism – Volume 2 – 1873 – Posner Memorial Collection – Carnegie Mellon University
- Joseph Larmor (1897) "On a dynamical theory of the electric and luminiferous medium", Phil. Trans. Roy. Soc. 190, 205–300 (third and last in a series of papers with the same name).
- Hendrik Lorentz (1899) "Simplified theory of electrical and optical phenomena in moving systems", Proc. Acad. Science Amsterdam, I, 427–43.
- Hendrik Lorentz (1904) "Electromagnetic phenomena in a system moving with any velocity less than that of light", Proc. Acad. Science Amsterdam, IV, 669–78.
- Henri Poincaré (1900) "La théorie de Lorentz et le Principe de Réaction", Archives Néerlandaises, V, 253–78.
- Henri Poincaré (1902) La Science et l'Hypothèse
- Henri Poincaré (1905) "Sur la dynamique de l'électron", Comptes rendus de l'Académie des Sciences, 140, 1504–8.
- Catt, Walton and Davidson. "The History of Displacement Current". Wireless World, March 1979.
External links
- Hazewinkel, Michiel, ed. (2001), "Maxwell equations", Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
- maxwells-equations.com — An intuitive tutorial of Maxwell's equations.
- Mathematical aspects of Maxwell's equation are discussed on the Dispersive PDE Wiki[permanent dead link].
Modern treatments
- Electromagnetism (ch. 11), B. Crowell, Fullerton College
- Lecture series: Relativity and electromagnetism, R. Fitzpatrick, University of Texas at Austin
- Electromagnetic waves from Maxwell's equations on Project PHYSNET.
- MIT Video Lecture Series (36 x 50 minute lectures) (in .mp4 format) – Electricity and Magnetism Taught by Professor Walter Lewin.
Other
$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$$
 https://en.wikipedia.org/wiki/Maxwell%27s_equations
https://en.wikipedia.org/wiki/Maxwell%27s_equations



















































![{\displaystyle {\begin{aligned}\partial _{[i}B_{jk]}&=\\\nabla _{[i}B_{jk]}&=0\\\partial _{[i}E_{j]}+{\frac {\partial B_{ij}}{\partial t}}&=\\\nabla _{[i}E_{j]}+{\frac {\partial B_{ij}}{\partial t}}&=0\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/75ac075f8b597a9b184015710692bc163993edab)

![{\displaystyle {\begin{aligned}B_{ij}&=\partial _{[i}A_{j]}\\&=\nabla _{[i}A_{j]}\\E_{i}&=-{\frac {\partial A_{i}}{\partial t}}-\partial _{i}\phi \\&=-{\frac {\partial A_{i}}{\partial t}}-\nabla _{i}\phi \\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/23f354c7207a4290ddf233fc754f9c5c8538685d)
![{\displaystyle {\begin{aligned}-{\frac {1}{\sqrt {h}}}\partial _{i}{\sqrt {h}}(\partial ^{i}\phi +{\frac {\partial A^{i}}{\partial t}})&=\\-\nabla _{i}\nabla ^{i}\phi -{\frac {\partial }{\partial t}}\nabla _{i}A^{i}&={\frac {\rho }{\epsilon _{0}}}\\-{\frac {1}{\sqrt {h}}}\partial _{i}({\sqrt {h}}h^{im}h^{jn}\partial _{[m}A_{n]})+{\frac {1}{c^{2}}}{\frac {\partial }{\partial t}}({\frac {\partial A^{j}}{\partial t}}+\partial ^{j}\phi )&=\\-\nabla _{i}\nabla ^{i}A^{j}+{\frac {1}{c^{2}}}{\frac {\partial ^{2}A^{j}}{\partial t^{2}}}+R_{i}^{j}A^{i}+\nabla ^{j}(\nabla _{i}A^{i}+{\frac {1}{c^{2}}}{\frac {\partial \phi }{\partial t}})&=\mu _{0}J^{j}\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c39e4049dae8b1c4a493ac711fc97b442cc1577f)
![{\displaystyle {\begin{aligned}B_{ij}&=\partial _{[i}A_{j]}\\&=\nabla _{[i}A_{j]}\\E_{i}&=-{\frac {\partial A_{i}}{\partial t}}-\partial _{i}\phi \\&=-{\frac {\partial A_{i}}{\partial t}}-\nabla _{i}\phi \\\nabla _{i}A^{i}&=-{\frac {1}{c^{2}}}{\frac {\partial \phi }{\partial t}}\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/87d9912526b84bab85ab01019f9f79ab508f1992)







![\partial _{[\alpha }F_{\beta \gamma ]}=0](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f11586830935cfd6dce389116d57ecec6cc70d2)

![{\displaystyle F_{\alpha \beta }=2\partial _{[\alpha }A_{\beta ]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c7fdf6910b5e5a6c20313f736a4ff965bbf55bf)
![{\displaystyle 2\partial _{\alpha }\partial ^{[\alpha }A^{\beta ]}=\mu _{0}J^{\beta }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df008f58c4109afbd135e583367b6c137768bd64)
![{\displaystyle {\begin{aligned}F_{\alpha \beta }&=2\partial _{[\alpha }A_{\beta ]}\\\partial _{\alpha }A^{\alpha }&=0\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab3e344d5194269842501ede8f8502b2880c42a8)

![{\begin{aligned}\partial _{[\alpha }F_{\beta \gamma ]}&=\\\nabla _{[\alpha }F_{\beta \gamma ]}&=0\end{aligned}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b3a9b258bb309cf1322cef45fe0622b5fcecae25)

![{\displaystyle {\begin{aligned}F_{\alpha \beta }&=2\partial _{[\alpha }A_{\beta ]}\\&=2\nabla _{[\alpha }A_{\beta ]}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/39d090d20ce9e7bd86a1b82a3658878d8a797fa8)
![{\displaystyle {\begin{aligned}{\frac {2}{\sqrt {-g}}}\partial _{\alpha }({\sqrt {-g}}g^{\alpha \mu }g^{\beta \nu }\partial _{[\mu }A_{\nu ]})&=\\2\nabla _{\alpha }(\nabla ^{[\alpha }A^{\beta ]})&=\mu _{0}J^{\beta }\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ae6dae90d0d85d51b8113e8e9d031388736b9ce1)
![{\displaystyle {\begin{aligned}F_{\alpha \beta }&=2\partial _{[\alpha }A_{\beta ]}\\&=2\nabla _{[\alpha }A_{\beta ]}\\\nabla _{\alpha }A^{\alpha }&=0\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/440ca267073e9b3f4b475e05a1d69a333a9bad4f)






